Every once in a while, a new discovery is made in science that is only partially-understood. Inevitably, this gets reported to the masses in a watered-down way by news writers who do not understand science, and there is a great cry: “The foundations of science are crumbling! Science discovers thing that is impossible to explain! Everything you know is wrong!” And, naturally, there are plenty of people who take this opportunity to tack on: “…therefore, there really must be a God!”
One example of this centers around the decades-long debate over quasi-crystals. To give you a sense of what quasi-crystals are and why they matter, I’d like to introduce you to the “Perplexing Poultry” game. This is a puzzle game in which you have a large collection of tiles that come in two shapes: two different (slightly mutant-looking) chicken shapes.
The game is quite simple: arrange the shapes in a tiling. In other words, fit them together into a pattern that covers the surface that you are working on with no gaps. You are familiar with “tiles,” of course, although most of the time they are not poultry: usually the pieces are squares or rectangles, or sometimes triangles and hexagons. There was a time when it was quite fashionable to cover floors this way.
But when you use the Perplexing Poultry tiles, you immediately realize that there is a problem here. It’s possible, but it’s extremely hard. You can put together the first several pieces very easily, of course. But as the pattern grows, it gets more and more difficult. You sometimes actually have to back-track, because you realize you have “worked your way into a corner.” In other words, you’ve built a pattern up part-way that makes a completely space-filling solution impossible: you have a gap that you cannot fill. That’s why this is interesting as a puzzle or a game: you cannot simply do it mechanically. You have to plan ahead, think about what you want the larger shape to look like. Picking the “next piece” isn’t just something you can do based on what you see on the board: you have to take into consideration the pattern produced by pieces that you have not yet put down.
So creating a Perplexing Poultry tiling is possible, but hard. It seems to require intelligence or planning. This is different from tiling a floor with, say, squares or hexagons. Those produce a repeating pattern, or in the language preferred by mathematicians, those tilings have “translational symmetry.” You can create them by following very simple rules. You could easily write a computer program to generate a repetitive pattern tiling, or you could even imagine some natural system following simple physical laws producing the same result.
The problem with Perplexing Poultry is that the pattern never repeats. Ever. No matter how big you make the tiling, you will never “start over” and be able to say: “OK, now I can just do the same thing again.” Instead, every single step of the way, you will have to follow the same complicated process of planning ahead, envisaging a pattern with no gaps, and trying to move forward… and backtracking if you make a mistake and force yourself into creating a “gap.”
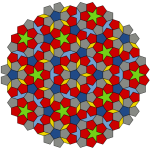This type of non-repeating pattern was first discovered by Roger Penrose in the 1970’s. As a result, they are called Penrose Tilings. The key features of a Penrose Tiling are 1) they completely fill the space with no gaps, 2) they are made up of a limited number of predefined shapes that are used over and over again, and 3) the pattern never, ever repeats. Penrose discovered that these tilings tend to happen when the pieces have five-fold symmetry (e.g. pentagons). You will notice that the Perplexing Poultry pieces are basically deformed pentagons.
Penrose Tilings can be radially symmetrical: in other words, they can have rotational symmetry (although they do not necessarily have this property, as you can see with the perplexing poultry). However, as you move from left to right (or top to bottom) they a completely non-repeating. You could go on literally indefinitely and never see the same pattern twice.
Now, let’s talk about crystals. Most crystals are regular tilings. They are made up of atoms that bond with each other so that they fit together like squares or hexagons and produce normal “tiling patterns.” This is actually what a “crystal” is: a tiling pattern of atoms. It is very repetitive, and it’s very easy for them to form using simple laws of physics. There is no “foreknowledge” or planning needed to make sure that no gaps appear. There would never need to be any “backtracking” in the creation of the pattern arising from the system growing into a pattern that could not be solved. Instead, each piece can fit into the system based only on what is already there, in a mindless and mechanical way, and the crystal will continue to grow.
In 1982, Dan Shechtman observed an electron diffraction pattern in an Al-Mn alloy which had been rapidly cooled after melting that appeared to have the properties of a Penrose tiling: a space-filling crystal made up of a limited set of elements that never repeated. He boldly entitled the paper “Metallic Phase with Long-Range Orientational Order and No Translational Symmetry” and declared that he had found a quasi-crystal: a crystal-like structure that was non-repeating. Plus, it had five-fold symmetry. Score!
His work was dismissed. He was mocked. He was even asked to leave his research group for defending his findings. He was called “wrong according to the textbook.” One of Dan’s fiercest critic was Linus Pauling (Nobel Prize in Chemistry & Nobel Peace Prize laureate), who reportedly once said, “There are no quasi-crystals, only quasi-scientists.” Other scientists either went through great efforts to explain how the data had been misinterpreted, or they ignored it altogether.
Eventually, his work was supported by other findings and by other scientists. Over the next 10 years, more and more people started accepting that quasi-crystals could be manufactured in the laboratory under certain conditions. In 1992 the International Union of Crystallography even altered its definition of a crystal, reducing it to the ability to produce a “clear-cut diffraction pattern” and acknowledging the possibility of the ordering to be either periodic or aperiodic. Finally, after more than a decade of methodical hunting, scientists reported finding the first natural quasi-crystal, a mineral found in the Khatyrka River in eastern Russia.
So almost 30 years after his initial paper on the subject, Dan Shechtman was awarded the 2011 Nobel Prize in Chemistry for his work on quasi-crystals. They really do exist.
But wait!
How is this possible? Didn’t our little Perplexing Poultry puzzle prove that these types of crystals cannot form based on simple mechanical rules? Haven’t we demonstrated that in order for quasi-crystals to form, there would have to be planning, and decisions, and that somehow a conscious mind would have to have an idea of what the final pattern looked like in order to make it happen?
Isn’t this proof, therefore, of intelligent design? Isn’t this proof that the basic foundation of science is completely cracking??????
No, it’s not.
It’s true that many scientists made the argument that quasi-crystals were impossible because it would require “action at a distance” or a global determination about what elements fit into what positions while that crystal was forming. But while it’s true that some scientists made those arguments, it’s also possible that those arguments were simply wrong.
In much the same way that it took almost three decades from the time when the term “quasi-crystal” was coined to the point where a naturally-occurring example of it was discovered, it sometimes takes time and effort to figure out how things are possible.
The first steps have already been taken. In 2008, Aaron Keys and Sharon Glotzer used a computer simulation to demonstrate how quasi-crystals could grow using only simple physical rules and “local information”: in other words, there didn’t have to be any planning entity who was “envisaging the whole pattern” in order to make it work. The basic mechanism has to do with the crystal forming in “clumps” or local clusters that then can maneuver to fit together.
This simulation is, I’m sure, just the first step in the development of a more sophisticated understanding of what types of processes are at work in the natural creation of quasi-crystals. It will produce deep and interesting insights about the mechanics involved in crystal formation, I’m sure.
But it’s not proof of a god.
This type of thing happens fairly often in science: there is a discovery that nobody can explain, non-scientists freak out and claim that it represents the complete failure of all science and proof that there is a god, and then science explains it.
That’s pretty much how science has worked, since the very beginning.
